Cosmic Microwave Background Statistics And Facts (2025)

Updated · Sep 08, 2025


WHAT WE HAVE ON THIS PAGE
- Introduction
- Editor’s Choice
- Where the Cosmic Microwave Background Came From
- Monopole Temperature and the Spectrum
- The Dipole
- Temperature Anisotropy Power Spectrum, Acoustic Peaks, and Damping
- Polarization, TE, and EE
- The Six Parameter CDM Fit From the Cosmic Microwave Background
- Lensing of the Cosmic Microwave Background
- What Each Parameter Does?
- Playbook Used
- Neutrinos, Relativistic Species and the Cosmic Microwave Background
- Known Quirks, Anomalies, and the H₀ Tension
- Ground and Space Experiments and What is Newest Right Now
- Background Pipeline
- Secondary Anisotropies and the Late-Time
- Why the Cosmic Microwave Background is Still the Best Engine in Cosmology
- Conclusion
Introduction
Cosmic Microwave Background Statistics: When we look up at the night sky, all we usually see are stars, planets, and maybe the unclear band of the Milky Way. But beyond that, there’s something far more important, a small light that has been shining across the universe for nearly 14 billion years. That is called the cosmic microwave background, and it is often described as the afterglow of the Big Bang.
So, what exactly is the cosmic microwave background? Think of it as a baby picture of the universe. Right after the Big Bang, the universe was extremely hot, dense, and filled with particles and light bouncing around in every direction. For the first 380,000 years, light could not travel freely because it was constantly scattered by electrons and protons.
But as the universe cooled, atoms began to form, and light was finally able to move freely through space. That ancient light has been traveling ever since, stretched into microwave radiation as the universe expanded, and today we can still detect it with sensitive instruments. The reason scientists get so excited about the cosmic microwave background is that it holds detailed information about the early universe. It tells us how old the universe is, what it is composed of, and even provides clues about how galaxies and stars eventually formed.
In this article, we will delve into the cosmic microwave background statistics. We’ll break everything down like measurements and discoveries, so you can see exactly why it is one of the most important pieces of evidence in modern cosmology. By the end of this article, you’ll understand why this microwave glow is the very foundation of our knowledge about the cosmos. Let’s get into it.
Editor’s Choice
- The cosmic microwave background is the oldest observable light in the universe, about 8 billion years old.
- It was released roughly 380,000 years after the Big Bang, when the universe cooled to about 3000 Kelvin.
- The present temperature of the cosmic microwave background is about 725 Kelvin, just above absolute zero.
- Tiny fluctuations in its temperature are only 1 part in 100,000, which seeded the formation of galaxies.
- The radiation peaks at a wavelength of 1.9 mm, placing it firmly in the microwave range of the spectrum.
- The energy density of the cosmic microwave background is about 0.25 eV/cm cube, making it a key component of the universe’s energy budget.
- Satellites like COBE (1989), WMAP (2001), and Planck (2009) have mapped the CMB in great detail, improving precision by more than 50 times.
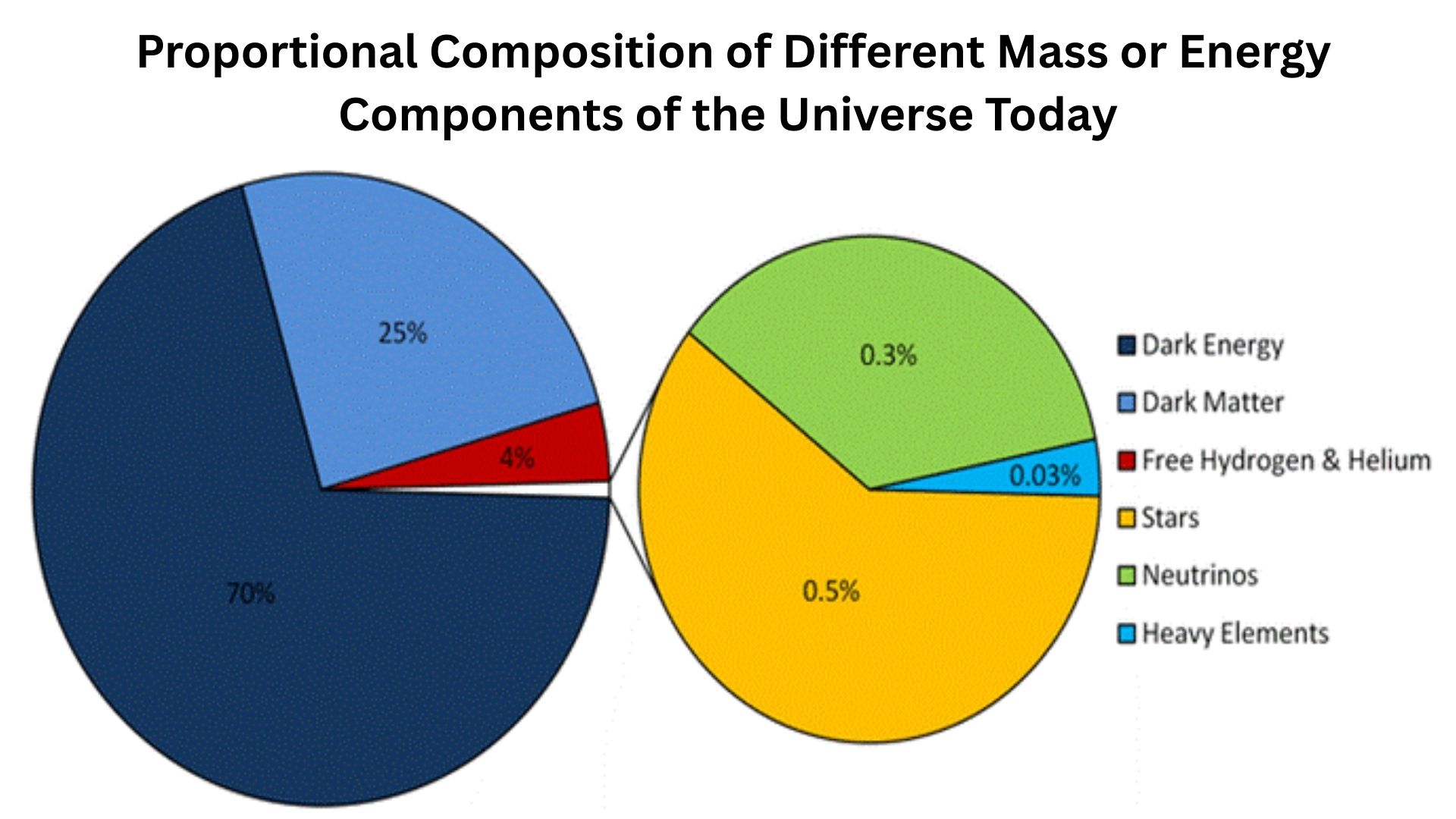
- Data from the cosmic microwave background shows the universe is made up of about 5% normal matter, 27% dark matter, and 68% dark energy.
- Measurements of the cosmic microwave background confirm the universe is geometrically flat with a margin of error less than 4%.
- The most precise maps of the cosmic microwave background come from the Planck satellite (2018), giving us the Hubble constant at 4 km/s/Mpc.
| Aspect | Metrics |
| Age of the universe (from CMB) |
13.8 billion years |
|
Release of CMB |
380,000 years after the Big Bang |
| Temperature then |
3000 K |
|
Current Temperature |
2,725 K |
| Wavelength Peak |
1.9 mm |
|
Temperature Fluctuations |
1 in 100,000 |
| Energy Density |
0.25 eV/cm cube |
|
Composition (from CMB data) |
5% matter, 27% dark matter, 68% dark energy |
| Flatness of the Universe |
0.4% deviation |
|
Best Map Source |
Planck (2018) |
| Hubble Constant (from CMB) |
67.4 km/s/Mpc |
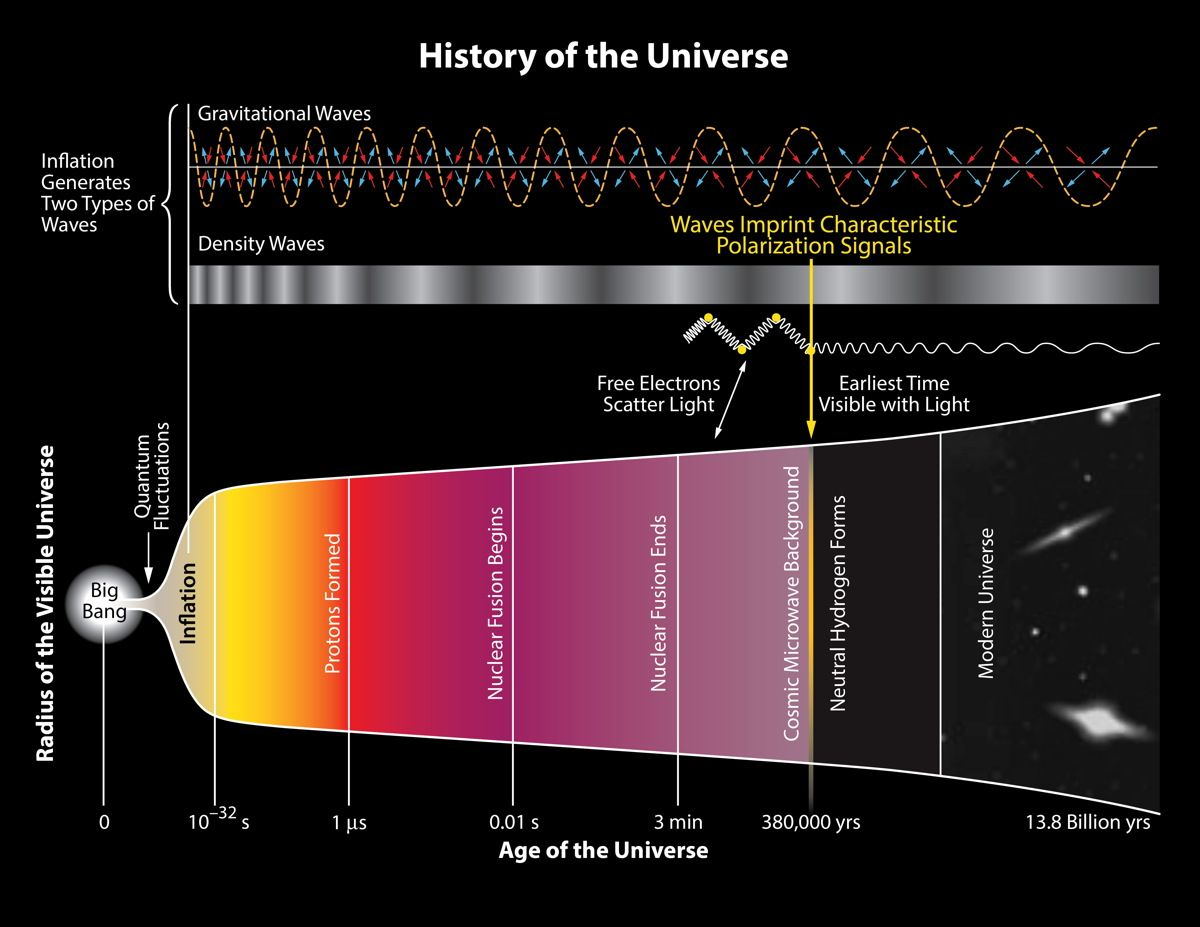
Where the Cosmic Microwave Background Came From
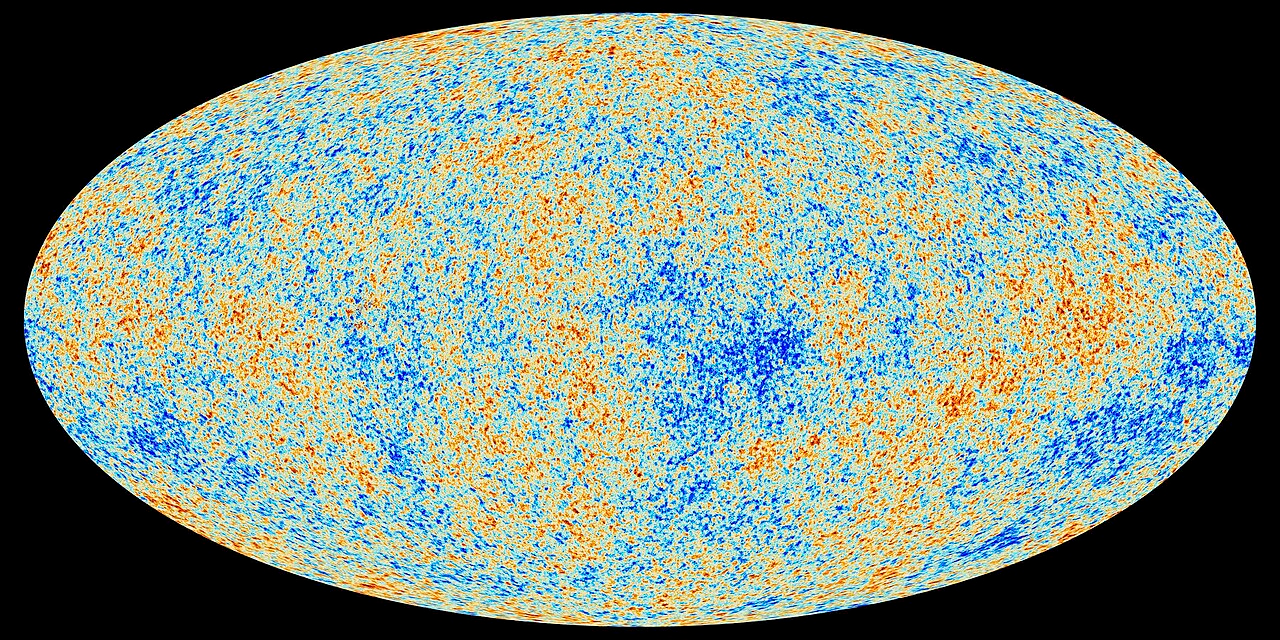
- The cosmic microwave background is the thermal afterglow of the early universe, released when the plasma of electrons and protons recombined into neutral hydrogen about 380,000 years after the Big Bang.
- That moment is often called last scattering, and it fixed the radiation we see today as a nearly perfect blackbody.
- The recombination redshift is roughly 1089 to 1090, which sets the distance and time to the cosmic microwave background surface.
- This number comes from precision fits to the temperature and polarization power spectra and is very stable across modern analyses.
| Quantity | Value |
| Age at last scattering | 0.38 million years |
| Redshift of last scattering | 1089.9 |
| Photon mean free path just before decoupling | Tiny compared with the horizon |
Monopole Temperature and the Spectrum
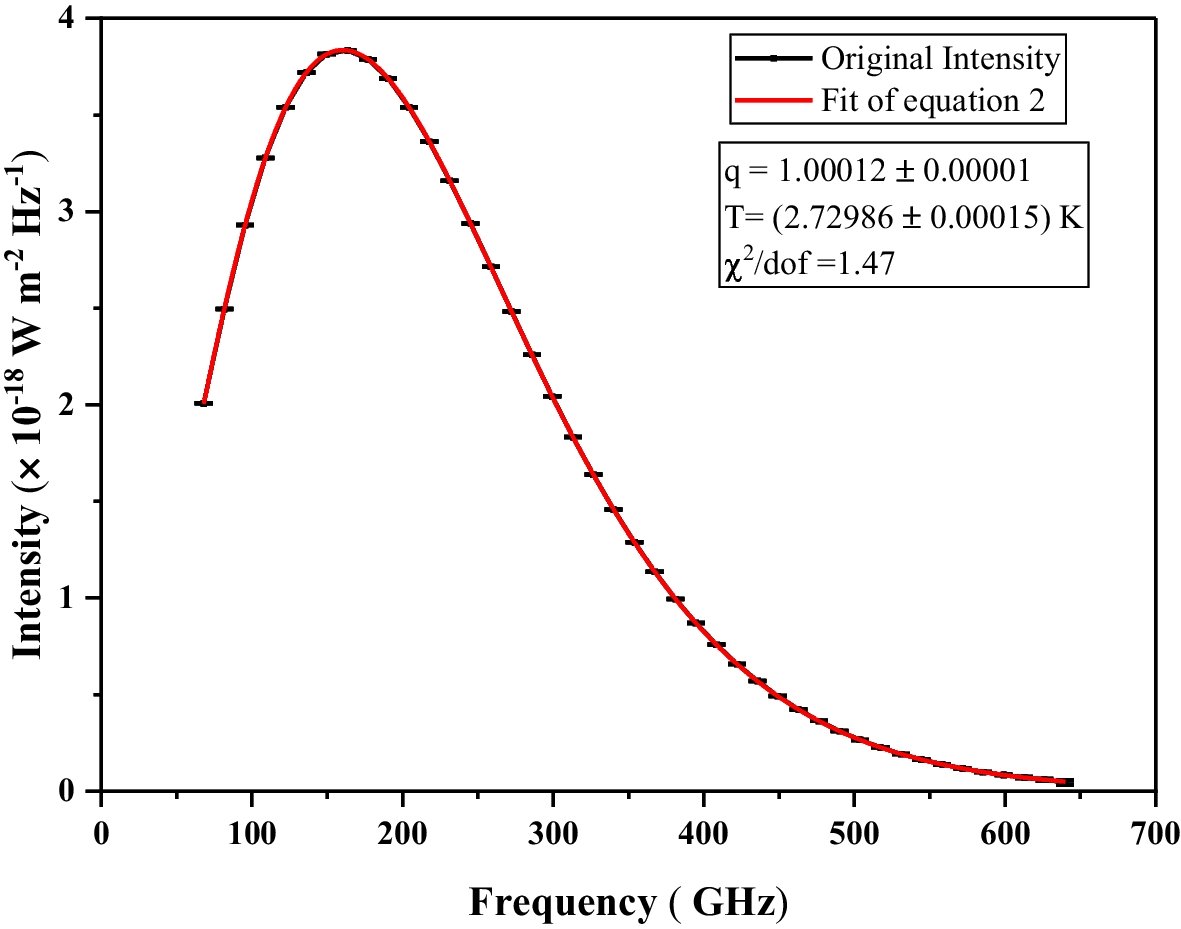
- The average sky temperature of the cosmic microwave background today is 2.72548 ± 0.00057 K.
- This came from COBE/FIRAS and remains the benchmark number, that 0.00057 K is not a type, the blackbody is that clean.
- Spectral distortions are extremely limited, FIRAS set type and y-type distortion limits around 9×10 power -5 and 1.5×10 power -5, which is why we say the cosmic microwave background is an almost perfect blackbody.
| Quantity | Value |
| Mean temperature | 2.72548 K |
| Distortion limit | 9×10 power -5 |
| Distortion limit | 1.5×10 power -5 |
The Dipole
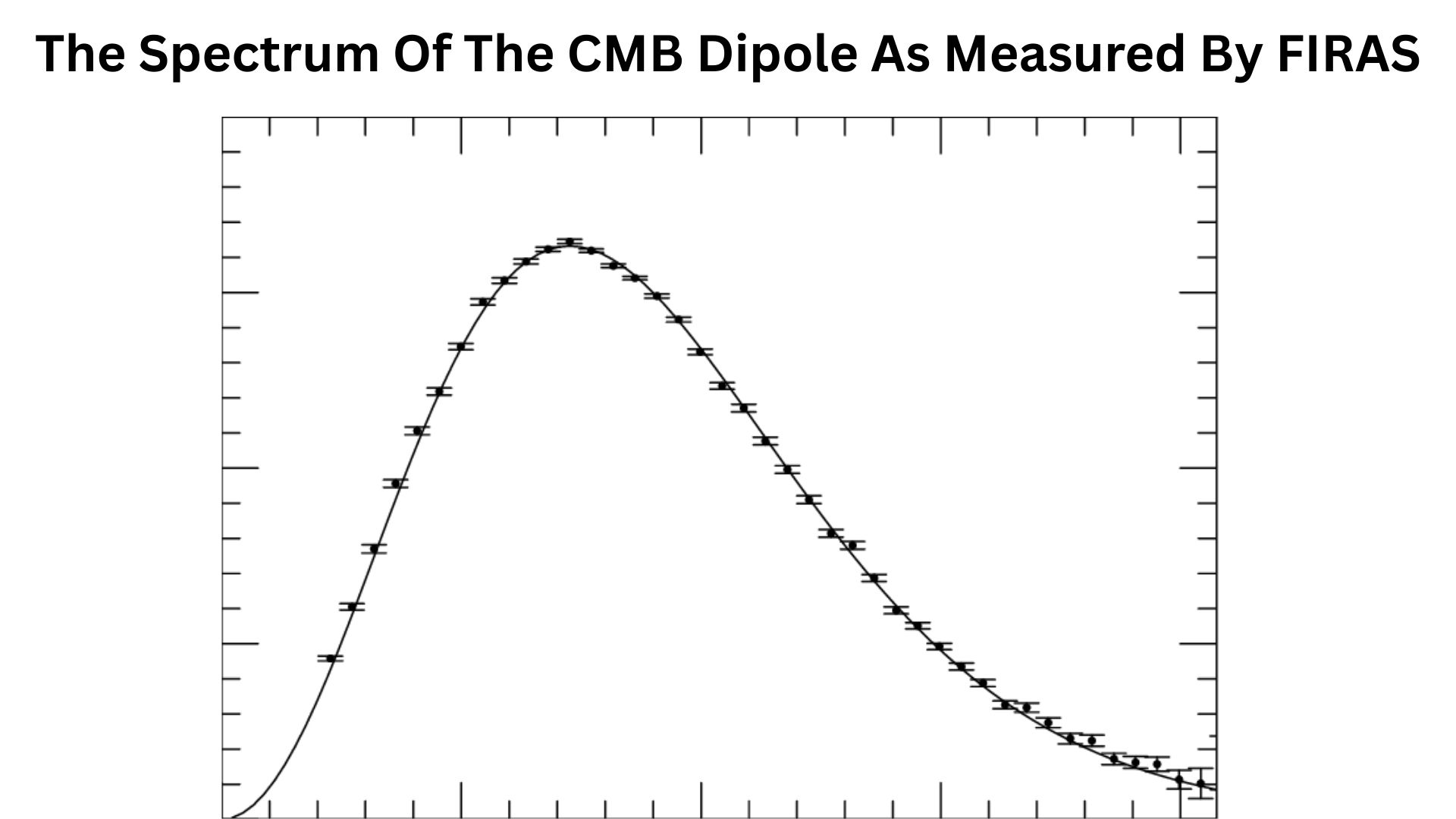
- The largest anisotropy is the dipole, amplitude of about 3.36 mK. It is almost entirely due to the solar system’s velocity relative to the cosmic microwave background rest frame, roughly 369 km, pointing toward Galactic coordinates near 264, b 48.
- Once you subtract the dipole, the remaining primary anisotropy is at the tens of microkelvin level.
- That is the statistically interesting part used to infer cosmology from the cosmic microwave background.
| Quantity | Value |
| Dipole amplitude | 3.36 mK |
| Solar System speed | 369 km |
| Dipole direction | 264 |
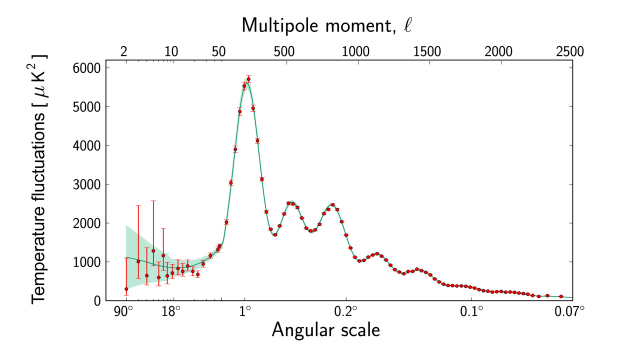
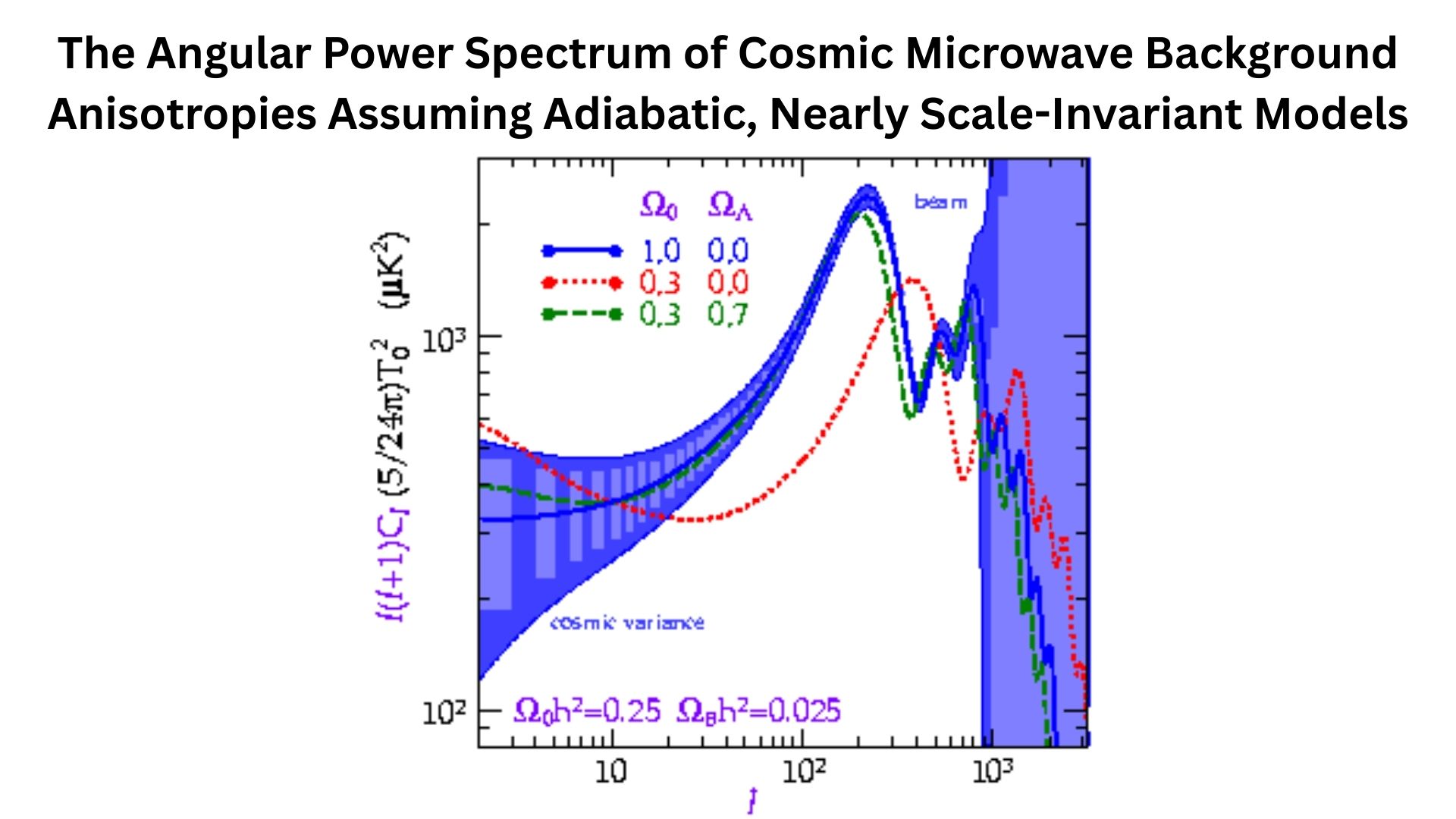
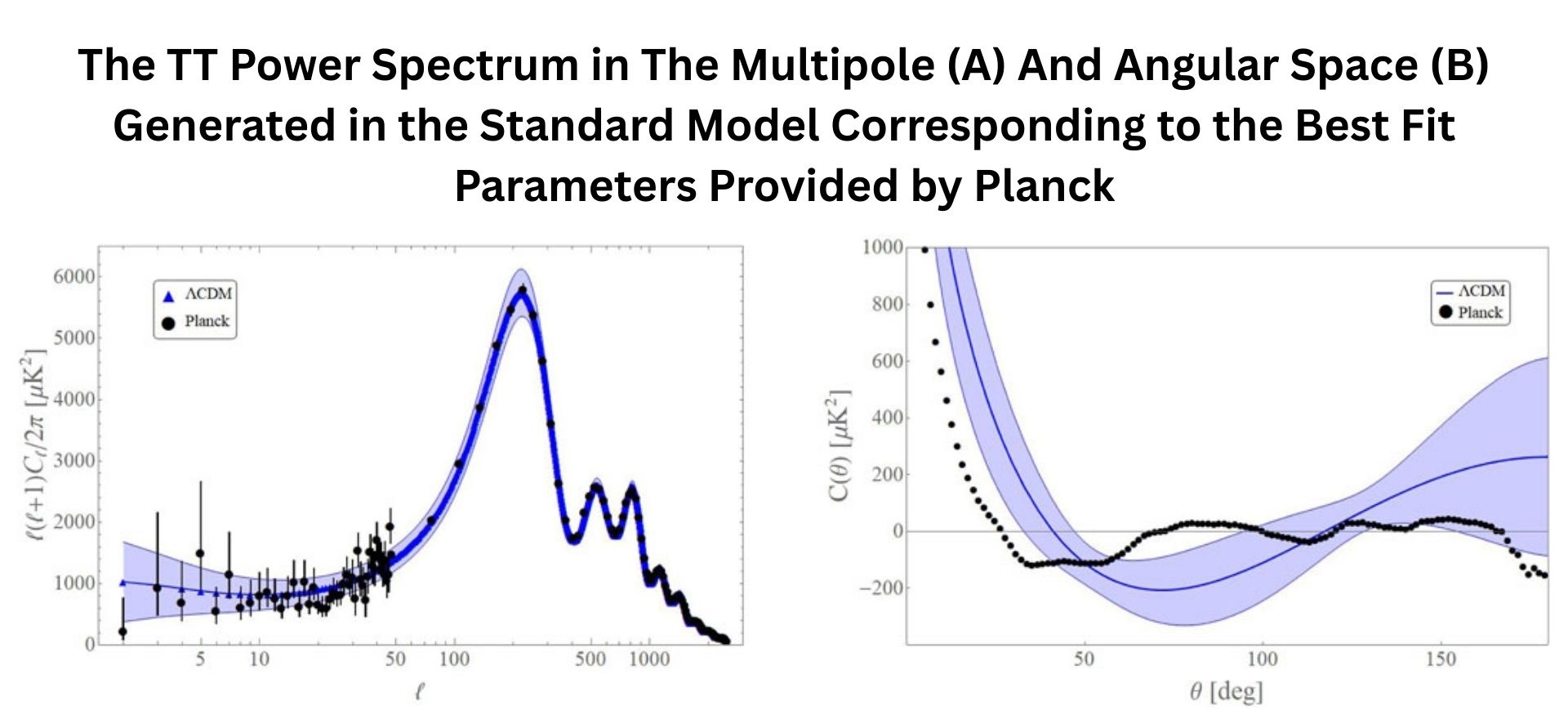
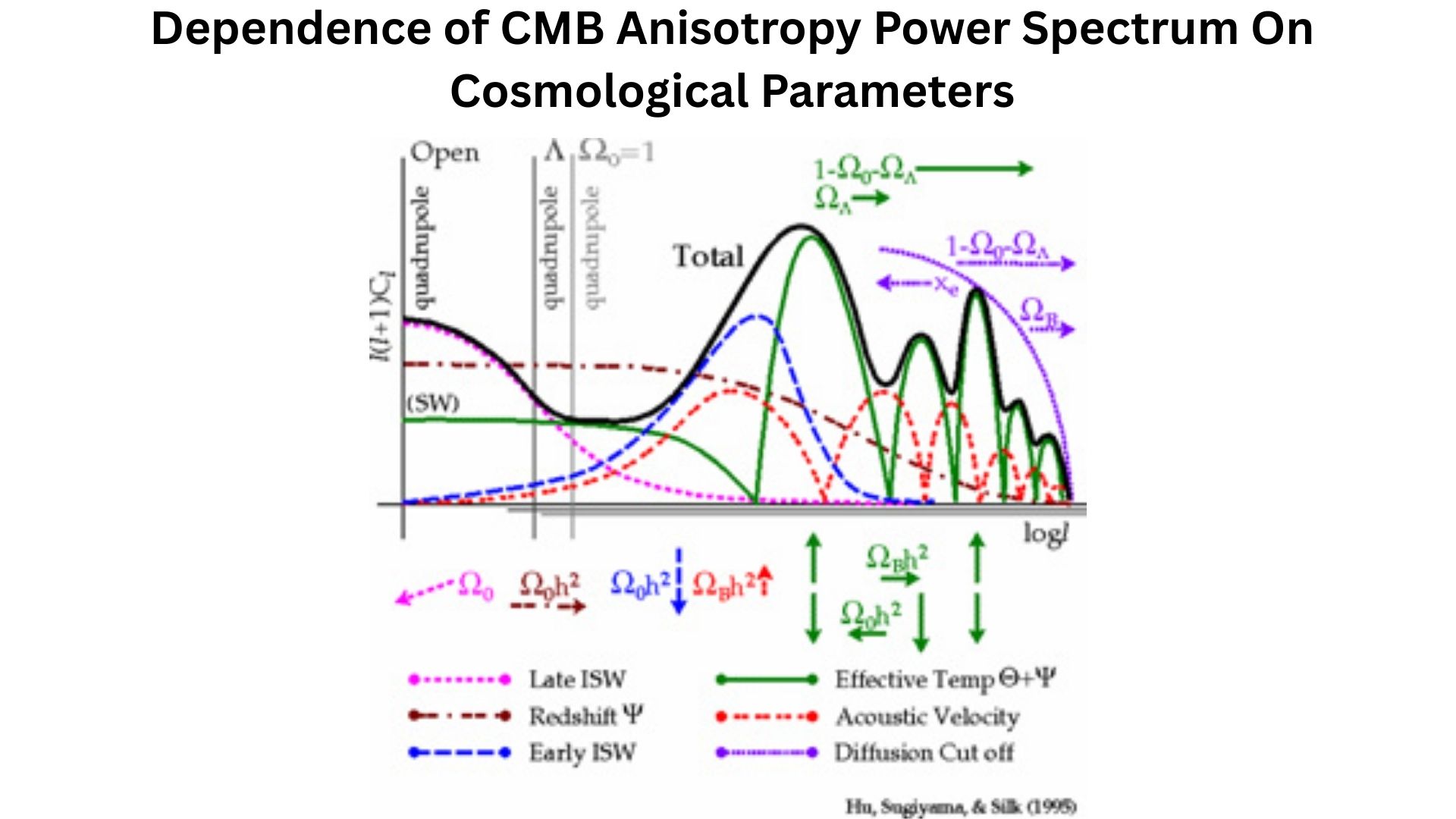
Temperature Anisotropy Power Spectrum, Acoustic Peaks, and Damping
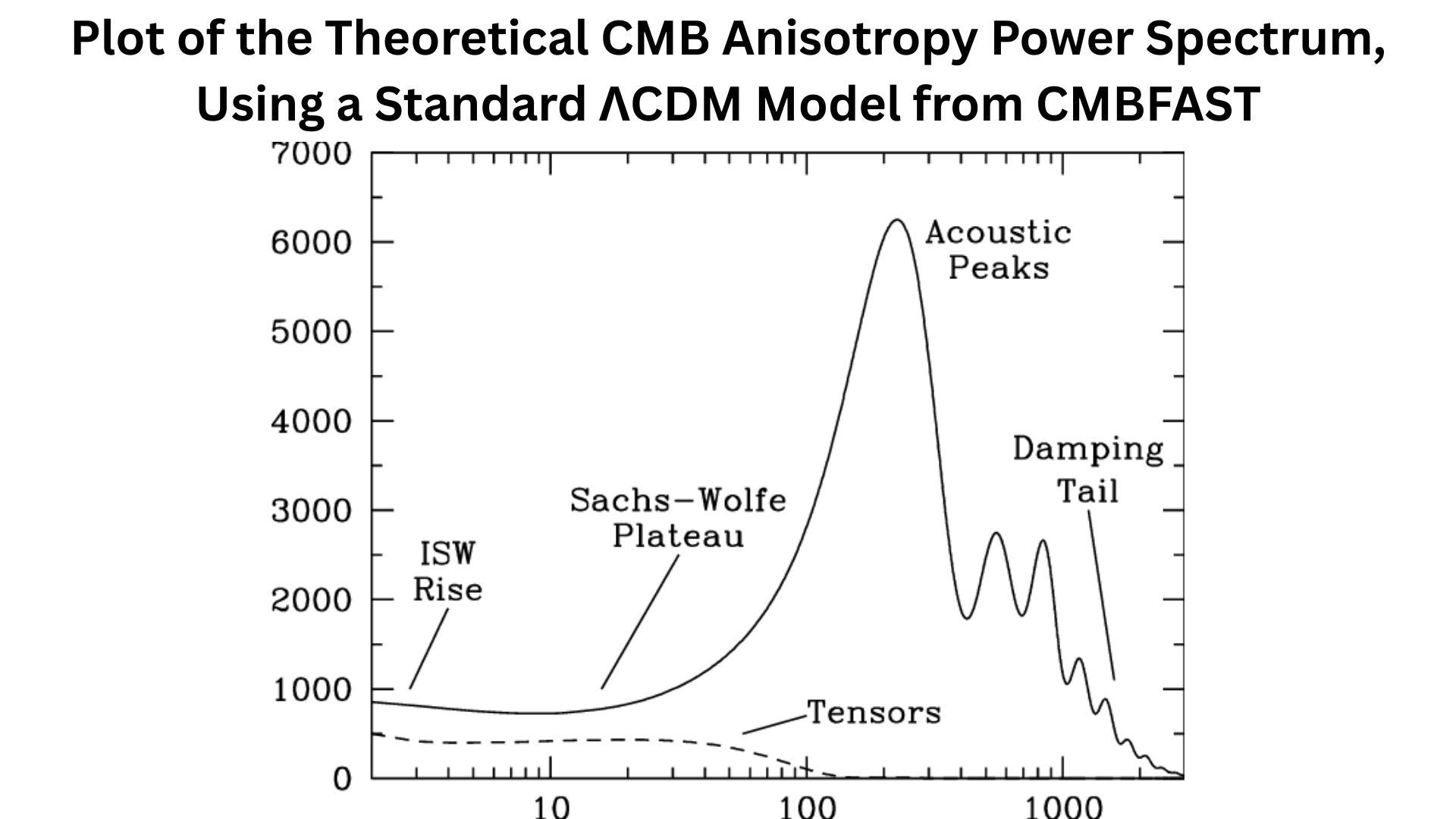
- We analyze the cosmic microwave background with spherical harmonics. Each multipole is like an angular wavenumber, roughly θ π/ℓ.
- The estimator variance is limited by cosmic variance, with fractional uncertainty √[2/(2ℓ+1)] for full sky, and it grows if you only see a fraction of the sky, f_sky.
- The first three temperature acoustic peaks are around ℓ 220, ℓ 540, and ℓ 800; the first peak position pins spatial geometry and the angular size of the sound horizon.
- The peak heights and odd-even pattern encode the baryon fraction and matter content through gravitational driving and baryon loading.
- The characteristic angular size of the acoustic scale is captured by 100 θ_ 1.0411, which means the sound horizon subtends roughly 0.6 degrees on the sky.
- Silk damping wipes out small-scale power.
- Photon diffusion at recombination acts like a Gaussian blur, so by ℓ 1500 to 2000, the power drops steeply.
- That damping tail is gold for measuring parameters like the spectral index and effective relativistic species.
| Feature | Metrics |
| First peak position | ℓ 220 |
| Second and third peaks | ℓ 540, ℓ 800 |
| Acoustic scale | 100 θ_* 1.041 |
| Small-scale damping | power falls for ℓ 1500 |
Polarization, TE, and EE
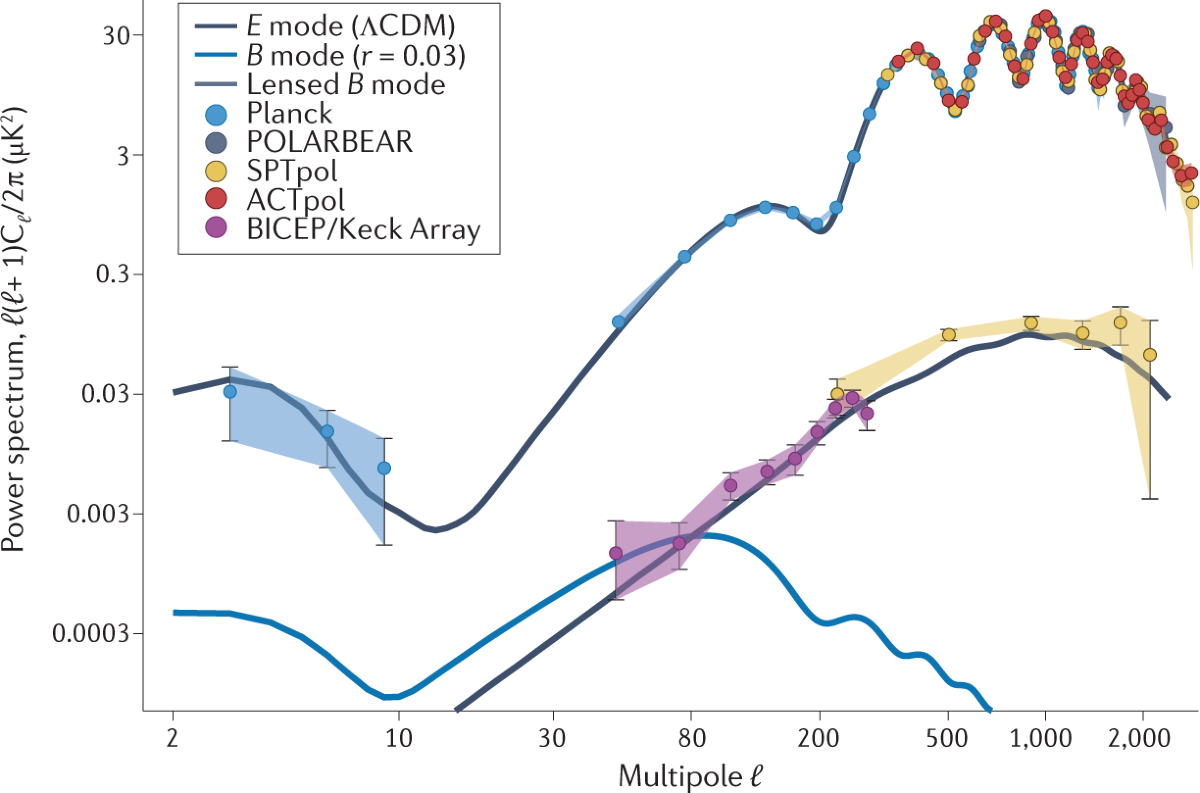
- Polarization splits into E-modes and B-modes. Scalar density perturbations generate E-modes at last scattering reionization.
- The TE cross-spectrum shows a clear alternating pattern that backs the adiabatic, coherent acoustic picture in the cosmic microwave background.
- Reionization leaves a large-scale E-mode bump, which constrains the optical depth τ . Modern full-sky analyses give τ 0.054 with a small error, corresponding to a midpoint reionization redshift z_re 7.5 to 8.0.
- Primordial gravitational waves would imprint B-models peaking around degree scales. The current 95% limit on the tensor-to-scalar ratio from BICEP/Keck BK18, combined with Planck and BAO in standard analyses, is 0.032 to 0,036 depending on the exact combo.
| Quantity | Metrics |
| Optical depth | 0.054 |
| Reionization redshift z_re | 7.7 |
| Tensor-to-scalar ratio about 95% | 0.02 to 0.036 |
The Six Parameter CDM Fit From the Cosmic Microwave Background
- The standard six parameters are Ω_b h², Ω_c h², θ_*, τ, n_s, ln(10¹⁰A_s). With high-precision TT, TE, EE plus lensing, you get percent-level constraints on each.
- Representative numbers from the definitive Planck 2018 analysis are H₀ 67.4 km s⁻¹ Mpc⁻¹, Ω_m 0.315, Ω_b h² 0.0224, Ω_c h² 0.120, n_s 0.965, τ 0.054, A_s 2.1×10⁻⁹ at k 0.05 Mpc⁻¹, σ₈ 0.811, and an age of 13.8 Gyr. These are the backbone statistics you see reused everywhere.
- One handy derived scale is the comoving sound horizon at photon decoupling, r_s, about 144 to 145 Mpc, which seeds the acoustic scale in both the cosmic microwave background and the BAO standard ruler.
| Parameter | Value |
| H₀ | 67.4 km s⁻¹ Mpc⁻¹ |
| Ω_m | 0.315 |
| Ω_b h² | 0.0224 |
| Ω_c h² | 0.120 |
| n_s | 0.965 |
| τ | 0.054 |
| A_s | 2.1×10⁻⁹ |
| σ₈ | 0.811 |
| r_s (decoupling) | 144 to 145 Mpc |
Lensing of the Cosmic Microwave Background
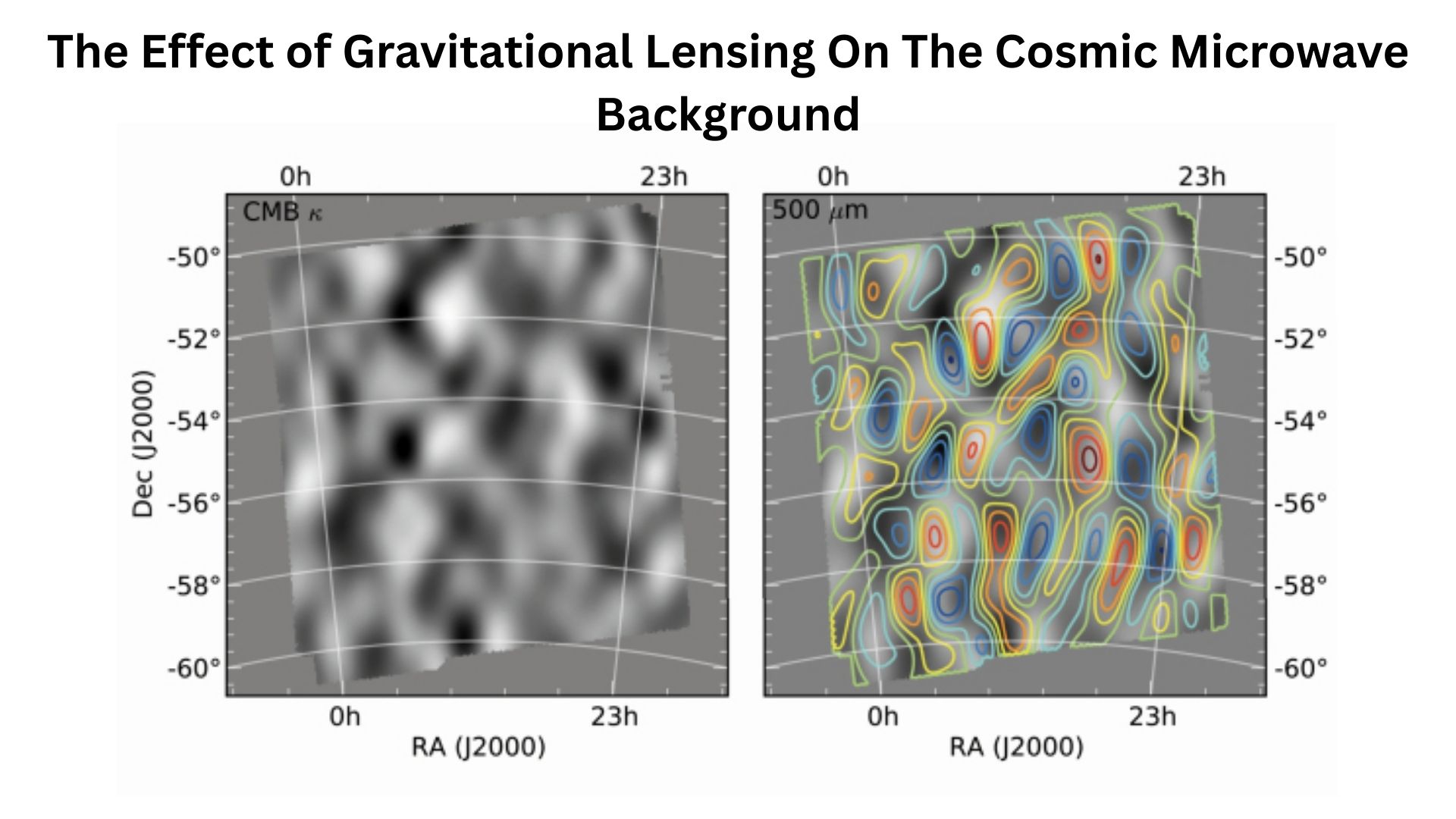
- Gravitational lensing remaps the cosmic microwave background by about 2 to 3 arcminutes RMS, smoothing acoustic peaks and generating small-scale B-models.
- It is detected at a very significant level, about 40 in Planck’s combined analysis.
- Planck’s lensing reconstruction by itself constrains structure growth, with numbers like σ₈ = 0.811 ± 0.019 and Ω_m 0.303 ± 0.017 when combined with simple priors or BAO.
- Modern ground-based experiments have mapped lensing at high resolution. ACT DR6 delivers a lensing map over 9400 deg, with precise constraints on growth parameters like S₈ and cross-correlations with large-scale structure.
| Lens | Status |
| Lensing detection significance | 40 (Planck) |
| Peak smoothing | A few percent |
| ACT DR6 lensing map | 9400 deg |
What Each Parameter Does?
- Ω_bh square up increases baryon loading, raises odd peaks relative to even peaks. You can literally read the baryon density from the odd-even peak contrast in the temperature spectrum.
- Ω_ch square up shifts the matter-radiation equality scale, moves the peaks horizontally, and changes the broad-band power. Damping tail and early Integrated Sachs Wolfe also respond to this.
- n_s up lifts small scales relative to large scales. A red tilt n_s 1 suppresses high ℓ power, which you see clearly in the damping tail of the Cosmic Microwave Background.
- τ up suppresses small-scale TT by e^{-2τ} and boosts large-scale EE due to rescattering after reionization. This is why low-ℓ polarization is crucial.
- θ_* moves the entire peak pattern horizontally. That parameter is pinned to ridiculous precision by the Cosmic Microwave Background, which is why the acoustic scale is the most precise ruler in cosmology.
| Parameter increase | Main spectral effect | Quick mental picture |
| Ω_b h² | Raises odd over even peaks | Extra inertia in photon-baryon fluid |
| Ω_c h² | Shifts equality, broadband tilt | Early expansion rate change |
| n_s | Tilts small vs large scales | Red vs Blue tilt |
| τ | Suppresses TT small scales, boosts EE large scales | Reionization imprints |
| θ_ | Slides peaks horizontally | Geometric ruler lock-in |
Playbook Used
- The data vector is typically D_ℓ = ℓ(ℓ+1)C_ℓ / 2π for TT, TE, EE, plus lensing C_L^{\phi\phi}. You build a Gaussian likelihood around those bandpowers with exact or approximate covariance, and fit ΛCDM parameters with MCMC.
- Cosmic variance is an absolute floor: fractional error on full-sky C_ℓ is √[2/(2ℓ+1)], and with f_sky sky fraction, you pay a 1/√1/f_sky penalty in the variance and add mode coupling. This is why all-sky datasets still matter for the largest scales.
| Concept | Formula or fact | Why it matters |
| Bandpower estimator | D_ℓ = ℓ(ℓ+1)C_ℓ/2π | Flattens the spectrum for visualization |
| Cosmic variance | Var(C_ℓ)/C_ℓ² 2/(2ℓ+1) | Sets the ultimate precision threshold |
| Sky fraction | Variance scales 1/f_sky | Partial sky adds correlations |
Neutrinos, Relativistic Species and the Cosmic Microwave Background
- The Cosmic Microwave Background is sensitive to the energy density in light relics through the expansion rate and diffusion scale. The effective number of relativistic species comes in as N_eff, and standard fits find N_eff consistent with 3.046 within about ±0.17 when combined with BAO.
- The sum of neutrino masses Σm_ν suppresses small-scale power. CMB plus BAO typically gives Σm_ν 0.12 eV at 95 % confidence in ΛCDM extensions where that parameter is free.
| Probe | Constraint |
| N_eff | 3.0 ± 0.17 |
| Σm_ν | 0.12 eV (95%) |
Known Quirks, Anomalies, and the H₀ Tension
- There is a mild preference in Planck TT for the phenomenological lensing amplitude A_L 1, around A_L 1.18 ± 0.065, which is about a 2 to 3σ curiosity.
- It does not show in the direct lensing reconstruction and looks frequency and mask-dependent, so most folks treat it as a statistical or systematic wrinkle, not hard evidence for new physics.
- Low-ℓ temperature power is a bit lower than the mean ΛCDM prediction, the quadrupole especially.
- The significance is limited by cosmic variance, which means it is not a slam-dunk anomaly, but it keeps coming up in discussions because it is visually obvious in full-sky maps.
- The H₀ tension is real in the sense that Cosmic Microwave Background fits prefer H₀ 67 to 68 km s⁻¹ Mpc⁻¹, while direct distance ladder estimates come in higher, near 73.
- That is a 4 to 5σ story depending on datasets. The Cosmic Microwave Background side is internally consistent and supported by BAO, which is why it is a big theoretical challenge.
| Quirk | Status | Comment |
| A_L 1 in TT | 2 to 3σ | Not seen in lensing reconstruction |
| Low quadrupole | Longstanding, low significance | Cosmic variance limited |
| H₀ tension | 67 vs 73 km s⁻¹ Mpc⁻¹ | Motivates new physics tests or systematics checks |
Ground and Space Experiments and What is Newest Right Now

- Satellite benchmarks are COBE for the spectrum, WMAP for the first precision cosmology with polarization, and Planck for sub-% ΛCDM. Planck 2018 remains the standard full-sky solution set for the Cosmic Microwave Background.
- High-resolution ground surveys target the small-scale Cosmic Microwave Background and lensing. ACT DR6 maps and power spectra cover up to 19,000 deg² with arcminute beams and deliver cutting-edge lensing and calibration for cross-correlations with galaxy surveys. This is the current, very active stream of new statistical results.
- On primordial gravitational waves, the combination of Planck and BICEP/Keck BK18 delivers the best current bounds on r, still no detection, with r limits in the 0.032 to 0.036 range at 95 percent. Next-gen experiments aim to push below r 0.01.
| Experiment | Key statistical contribution |
| Planck | Full-sky TT, TE, EE, lensing |
| ACT DR6 | High-res T, E maps and lensing |
| BICEP/Keck | Degree-scale B-modes |
Background Pipeline
- Mapmaking: start with timestreams, calibrate with planets and dipole, deconvolve beams, filter atmospheric 1/f noise for ground data, then coadd into multi-frequency maps. Polarization angles are calibrated with polarized sources, half-wave plates, or self-calibration using the TB and EB null conditions.
- Component separation: model synchrotron and thermal dust with multi-frequency SEDs, clean to residuals at the few microkelvin level. This is what lets the primary Cosmic Microwave Background signal dominate in the 70 to 150 GHz window.
- Bandpowers and covariances: pseudo-C_ℓ or maximum-likelihood power spectra, null tests by splitting data by time, scan, detector set. Cross-spectra between splits remove noise bias. Covariances include sample variance, noise, beam, calibration, and masking.
- Likelihood and MCMC: plug TT, TE, EE, and lensing into a Gaussian or semi-analytic likelihood, then sample ΛCDM plus extensions. Derived parameters and distances follow once the chain stabilizes.
| Step | Numerical reality |
| Calibration | Absolute gain tied to the CMB dipole and planets |
| Foregrounds | Dust and synchrotron cleaned down to a few μK |
| Covariance | Includes noise, beam, mask, and mode-coupling |
| Sampling | Millions of likelihood calls across parameters |
Secondary Anisotropies and the Late-Time
- Integrated Sachs-Wolfe at ℓ 20 is sensitive to dark energy at late times. It is small in temperature, hard to extract without cross-correlating with large-scale structure surveys, but it is there and accounted for in precise fits.
- Thermal and kinetic SZ effects add small-scale power that grows toward ℓ 3000 and beyond, especially at 150 and 220 GHz.
- Modern pipelines model and marginalize over SZ templates while fitting the damping tail. The numbers are a few μK² at those ℓ in TT, enough that you cannot ignore them when extracting high-ℓ statistics.
| Effect | Scale | Treatment |
| ISW | ℓ 20 | Small TT feature, cross-correlate with galaxies |
| tSZ, kSZ | ℓ 2000 to 5000 | Template-marginalized in TT, multi-band leverage |
Why the Cosmic Microwave Background is Still the Best Engine in Cosmology
- Raw precision. A single number like 100 θ_* is measured at the 3×10⁻⁴ level. That level of geometric control is why BAO and supernovae can be tied down so tightly once you impose the Cosmic Microwave Background prior.
- Consistency checks. You can measure the same physics in independent ways. For example, the Cosmic Microwave Background damping tail, the lensing reconstruction, and the smoothing of acoustic peaks all agree on structure growth to % levels.
| Strength | Example |
| Geometric precision | Acoustic scale and distance ladder anchoring |
| Redundancy | Lensing smoothing vs direct spectrum |
| Cross-checks | With BAO, RSD, and supernovae datasets |
Conclusion
So, overall, the cosmic microwave background is the clearest window we have into the early universe. From its tiny fluctuations to its precise temperature, every detail helps us understand how everything we see today first began.
By studying this cosmic microwave background statistics, scientists continue to refine our knowledge about the universe’s age, shape, and future. If you found this guide helpful and want to explore more about space, cosmology, and the science behind the universe, stay connected and keep reading. I hope you like this article. If you found any errors or have any questions, kindly let me know in the comments section. Thankyou.
FAQ.
The Cosmic Microwave Background is the oldest light in the universe, left over from the Big Bang. It is faint microwave radiation that fills the entire sky and tells us how the universe began.
The Cosmic Microwave Background is about 13.8 billion years old, dating back to the time when the universe was only 380,000 years old.
It helps scientists measure the age, shape, and composition of the universe. It also explains how galaxies and stars were formed from small fluctuations in the early universe.
It was discovered accidentally in 1965 by Arno Penzias and Robert Wilson, who later won the Nobel Prize for their work.
Today, the Cosmic Microwave Background has a temperature of about 2.725 Kelvin, just above absolute zero.
No, humans cannot see it with their naked eyes. It can only be detected with special microwave instruments and satellites.
Major satellites include COBE (1989), WMAP (2001), and Planck (2009). Planck gave the most detailed map in 2018.
It shows that the universe is made of about 5% normal matter, 27% dark matter, and 68% dark energy.
Yes, the Cosmic Microwave Background is one of the strongest pieces of evidence for the Big Bang theory.
It will always exist, but over trillions of years, as the universe keeps expanding, its radiation will stretch further and become even colder and harder to detect.

Rohan is a senior editor at Sci-Tech Today with extensive knowledge of digital marketing, SEO, and social media optimization (SMO). He is skilled at creating and editing detailed articles filled with accurate statistics that readers find valuable. As a senior editor, Rohan carefully reviews and quality-checks content from multiple writers before it is published. Additionally, he creates infographics to accompany the statistics, making the information easier to understand and more engaging for readers. Rohan's dedication ensures that Sci-Tech Today delivers high-quality and informative content to its audience.








